Given n and m which are the dimensions of a matrix initialized by zeros and given an array indices where indices[i] = [ri, ci]. For each pair of [ri, ci] you have to increment all cells in row ri and column ci by 1.
Return the number of cells with odd values in the matrix after applying the increment to all indices.
Example 1:
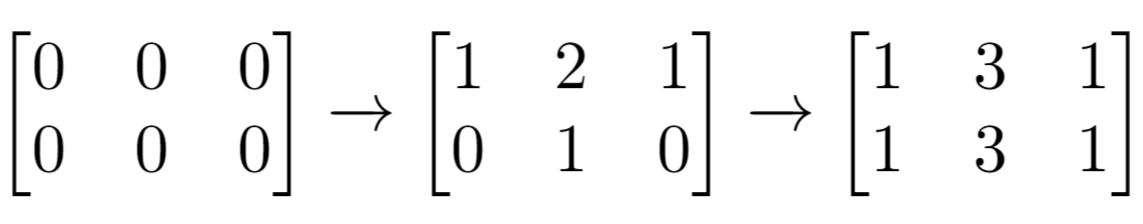
Input: n = 2, m = 3, indices = [[0,1],[1,1]] Output: 6 Explanation: Initial matrix = [[0,0,0],[0,0,0]]. After applying first increment it becomes [[1,2,1],[0,1,0]]. The final matrix will be [[1,3,1],[1,3,1]] which contains 6 odd numbers.
Example 2:
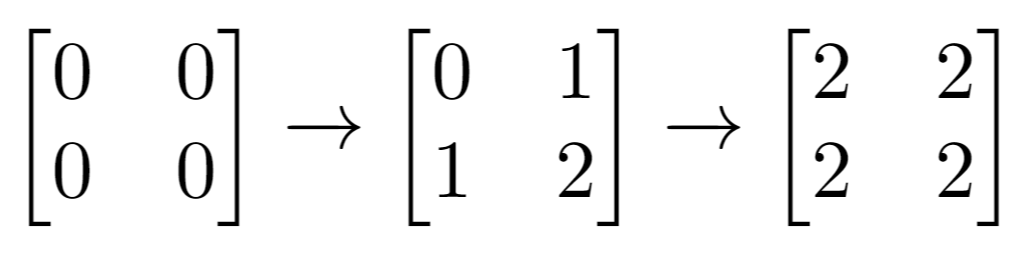
Input: n = 2, m = 2, indices = [[1,1],[0,0]] Output: 0 Explanation: Final matrix = [[2,2],[2,2]]. There is no odd number in the final matrix.
Constraints:
1 <= n <= 501 <= m <= 501 <= indices.length <= 1000 <= indices[i][0] < n0 <= indices[i][1] < m
A:
这个题目,因为m,n 都比较小,可以考虑用2D 的brute force解决
下面这个解法, 利用了奇偶性。
class Solution { public: int oddCells(int n, int m, vector<vector<int>>& indices) { int tmp = n; // because the given row, and col is unusual n = m; m = tmp; vector<int> rowChangedTime(m,0); vector<int> colChangedTime(n,0); for(auto & v: indices){ rowChangedTime[v[0]] = 1 - rowChangedTime[v[0]]; colChangedTime[v[1]] = 1 - colChangedTime[v[1]]; } int nRowAs1 = accumulate(rowChangedTime.begin(), rowChangedTime.end(), 0); int nColAs1 = accumulate(colChangedTime.begin(), colChangedTime.end(), 0); return nRowAs1 * n + nColAs1 * m - 2*nColAs1*nRowAs1; } };
No comments:
Post a Comment