Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.
Since the answer may be too large, return it modulo 10^9 + 7.
Example 1:
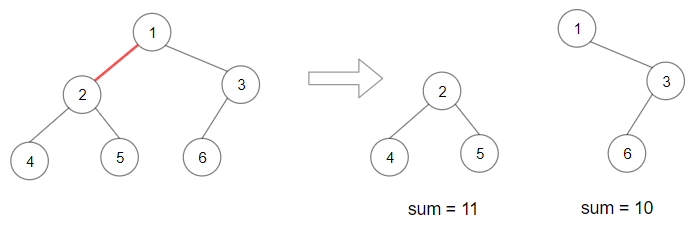
Input: root = [1,2,3,4,5,6] Output: 110 Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)
Example 2:
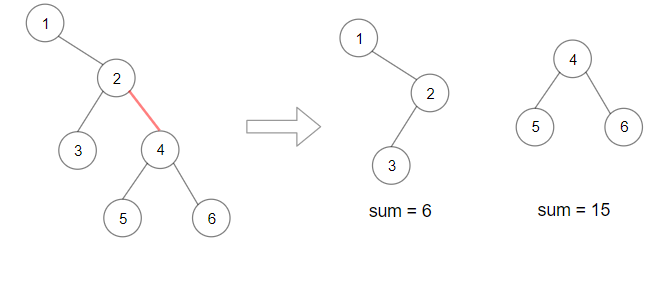
Input: root = [1,null,2,3,4,null,null,5,6] Output: 90 Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)
Example 3:
Input: root = [2,3,9,10,7,8,6,5,4,11,1] Output: 1025
Example 4:
Input: root = [1,1] Output: 1
Constraints:
- Each tree has at most
50000nodes and at least2nodes. - Each node's value is between
[1, 10000].
A:
递归,没什么好说的。
需要注意的的是, int 类型的相乘, 一定要用long ,防止overflow.
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int maxProduct(TreeNode* root) { int modulo = pow(10,9)+7; // INT is 32 bit vector<int> sums; int total = helper(root, sums, true);//long is 64 bit on 64 bit OS,(but 32 on linux 32-bit) long res = INT_MIN; for(auto v : sums){ res = max(res, (long(v) * (total -v))); } return int(res%modulo); } private: int helper(TreeNode* root, vector<int> & S, bool isRoot){ if(not root) return 0; int curSum = root->val + helper(root->left,S,false) + helper(root->right,S,false); if(not isRoot) S.push_back(curSum); return curSum; } };
ERRORS:
肏,这里犯了一个很傻的错误。
自己一开始都设成int 类型,因此为了不overflow, 就
for(auto v : sums){ res = max(res, (long(v) * (total -v))%modulo); }
这样,结果是不对的~~~~~~~~~~~~~
No comments:
Post a Comment