Given the root of a binary tree, find the largest subtree, which is also a Binary Search Tree (BST), where the largest means subtree has the largest number of nodes.
A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties:
- The left subtree values are less than the value of their parent (root) node's value.
- The right subtree values are greater than the value of their parent (root) node's value.
Note: A subtree must include all of its descendants.
Follow up: Can you figure out ways to solve it with O(n) time complexity?
Example 1:
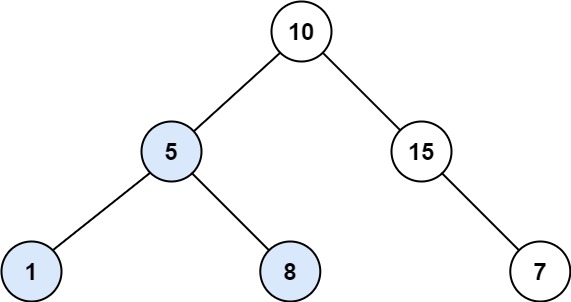
Input: root = [10,5,15,1,8,null,7] Output: 3 Explanation: The Largest BST Subtree in this case is the highlighted one. The return value is the subtree's size, which is 3.
Example 2:
Input: root = [4,2,7,2,3,5,null,2,null,null,null,null,null,1] Output: 2
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -104 <= Node.val <= 104
A:
这个一开始理解错误, 以为是要 root value with largest mean of BST呢
其实挺简单的。 就是利用 C++ 的 pass by reference 来update 最终结果
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int largestBSTSubtree(TreeNode* root) { if (not root) // shall never hit return 0; int largestCount = 0; int minVal = INT_MAX, maxVal = INT_MIN; int count = 0; helper(root, minVal, maxVal, count, largestCount); return largestCount; } private: bool helper(TreeNode* root, int& minValue, int& maxValue, int& count, int& largestCount) { if (not root) { return true; } int leftMin = INT_MAX, leftMax = INT_MIN; int leftCount = 0; bool isLeftBST = helper(root->left, leftMin, leftMax, leftCount, largestCount); int rightMin = INT_MAX, rightMax = INT_MIN; int rightCount = 0; bool isRightBST = helper(root->right, rightMin, rightMax, rightCount, largestCount); if (isLeftBST && isRightBST && root->val > leftMax && root->val < rightMin) { count = 1 + leftCount + rightCount; if (count > largestCount) { largestCount = count; } minValue = root->left ? leftMin : root->val; maxValue = root->right? rightMax : root->val; return true; } return false; } };
No comments:
Post a Comment