606. Construct String from Binary Tree -------E

Given the root node of a binary tree, your task is to create a string representation of the tree following a specific set of formatting rules. The representation should be based on a preorder traversal of the binary tree and must adhere to the following guidelines:

• Node Representation: Each node in the tree should be represented by its integer value.

• Parentheses for Children: If a node has at least one child (either left or right), its children should be represented inside parentheses. Specifically:

  • If a node has a left child, the value of the left child should be enclosed in parentheses immediately following the node's value.
  • If a node has a right child, the value of the right child should also be enclosed in parentheses. The parentheses for the right child should follow those of the left child.

• Omitting Empty Parentheses: Any empty parentheses pairs (i.e., ()) should be omitted from the final string representation of the tree, with one specific exception: when a node has a right child but no left child. In such cases, you must include an empty pair of parentheses to indicate the absence of the left child. This ensures that the one-to-one mapping between the string representation and the original binary tree structure is maintained.

  In summary, empty parentheses pairs should be omitted when a node has only a left child or no children. However, when a node has a right child but no left child, an empty pair of parentheses must precede the representation of the right child to reflect the tree's structure accurately.

 

Example 1:

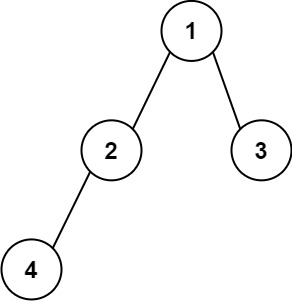
Input: root = [1,2,3,4]
Output: "1(2(4))(3)"
Explanation: Originally, it needs to be "1(2(4)())(3()())", but you need to omit all the empty parenthesis pairs. And it will be "1(2(4))(3)".

Example 2:

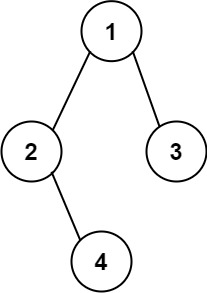
Input: root = [1,2,3,null,4]
Output: "1(2()(4))(3)"
Explanation: Almost the same as the first example, except the () after 2 is necessary to indicate the absence of a left child for 2 and the presence of a right child.

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -1000 <= Node.val <= 1000

A:

关键是仔细分析理解，从树的角度来看，如果只有左子树，那么右子树可以不管

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string tree2str(TreeNode* t) {
        if(t == nullptr)
            return "";
        if(t->left == nullptr && t->right == nullptr)
            return to_string(t->val);
        else if(t->right == nullptr)
            return to_string(t->val) + "(" + tree2str(t->left) + ")";
        else 
            return to_string(t->val) + "(" + tree2str(t->left) + ")" + "(" + tree2str(t->right) + ")";
    }
};

---------------这次，为了谨慎起见， 确保root不为null----------------

/**

* Definition for a binary tree node.

* struct TreeNode {

* int val;

* TreeNode *left;

* TreeNode *right;

* TreeNode() : val(0), left(nullptr), right(nullptr) {}

* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}

* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}

* };

*/

class Solution {

public:

string tree2str(TreeNode* root) {// root is not null

if(!root->left && !root->right){

return to_string(root->val);

}else if(!root->left && root->right){

return to_string(root->val)+"()"+"(" + tree2str(root->right) +")";

}else if(root->left && !root->right){

return to_string(root->val)+ "(" + tree2str(root->left) +")";

}else{

return to_string(root->val)+ "(" + tree2str(root->left) +")("+ tree2str(root->right) +")";

}

}

};