There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
- There are no self-edges (
graph[u]does not containu). - There are no parallel edges (
graph[u]does not contain duplicate values). - If
vis ingraph[u], thenuis ingraph[v](the graph is undirected). - The graph may not be connected, meaning there may be two nodes
uandvsuch that there is no path between them.
A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
Return true if and only if it is bipartite.
Example 1:
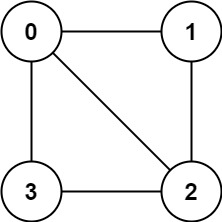
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]] Output: false Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]] Output: true Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Constraints:
graph.length == n1 <= n <= 1000 <= graph[u].length < n0 <= graph[u][i] <= n - 1graph[u]does not containu.- All the values of
graph[u]are unique. - If
graph[u]containsv, thengraph[v]containsu.
A:
class Solution { public: bool isBipartite(vector<vector<int>>& graph) { int n = graph.size(); vector<int> color(n,-1); // 0 as one color, 1 as another, and -1 as no-decided for(int i =0;i<n;i++){ if(color[i] >= 0) // already visited continue; color[i] = 1; // found a new connected component queue<int> Q; Q.push(i); while(!Q.empty()){ int start = Q.front(); Q.pop(); for(auto end : graph[start]){ if(color[end] == color[start]) return false; else if(color[end]== -1){ color[end] = 1 - color[start]; Q.push(end); } } } } return true; } };
注意QUEUE的应用。 (我一直以来都喜欢用2个 layer 但是那样需要拷贝一下,又空间的损失)
class Solution {
public:
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size(); // color the nodes
vector<int> Color(n, -1); // 0(white). and 1 for black
for (int i = 0; i < n; i++) {
int nextColor;
if(Color[i] < 0){
Color[i] = 0;
nextColor = 1;
}else{
nextColor = 1-Color[i];
}
for(auto id2 : graph[i]){
if(Color[id2] < 0 || Color[id2] == nextColor){
Color[id2] = nextColor;
}else{
return false;
}
}
}
return true;
}
};
上面这样是不对的。 自己考虑下,为什么。 (可以跟上上次的解法对比)

No comments:
Post a Comment