812. Largest Triangle Area ----------E

Q:

You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.

Example:
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2
Explanation: 
The five points are show in the figure below. The red triangle is the largest.

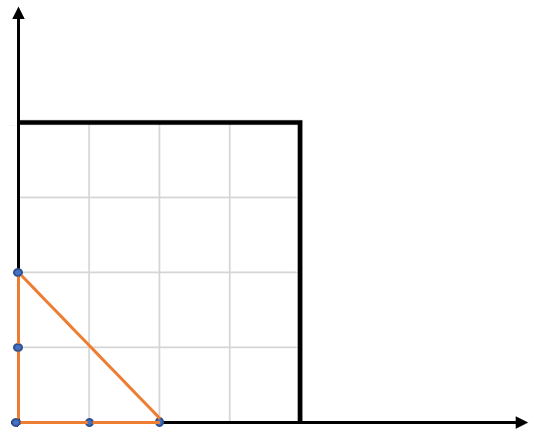
Notes:

• 3 <= points.length <= 50.
• No points will be duplicated.
•  -50 <= points[i][j] <= 50.
• Answers within 10^-6 of the true value will be accepted as correct.

A:

关键是   

Heron's formula

class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) {
        int n = points.size();
        double res = 0;
        for(int i =0;i<n-2;i++)
            for(int j = i+1;j<n-1;j++)
                for(int k = j+1; k<n; k++)
                {
                    res = max(res, getArea(points[i], points[j], points[k]));
                }
        return res;
    }
private:
    double getArea(vector<int>& A, vector<int> & B, vector<int> & C){
        double a = sqrt(  pow(A[0] -B[0], 2)  + pow(A[1] -B[1], 2) );
        double b = sqrt(  pow(A[0] -C[0], 2)  + pow(A[1] -C[1], 2) );
        double c = sqrt(  pow(B[0] -C[0], 2)  + pow(B[1] -C[1], 2) );
        double area = 0.25 * sqrt( (a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c) );
        return area;
    }
};