1007. Minimum Domino Rotations For Equal Row ---M

 In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the i-th domino.  (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the i-th domino, so that A[i] and B[i] swap values.

Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.

If it cannot be done, return -1.

 

Example 1:

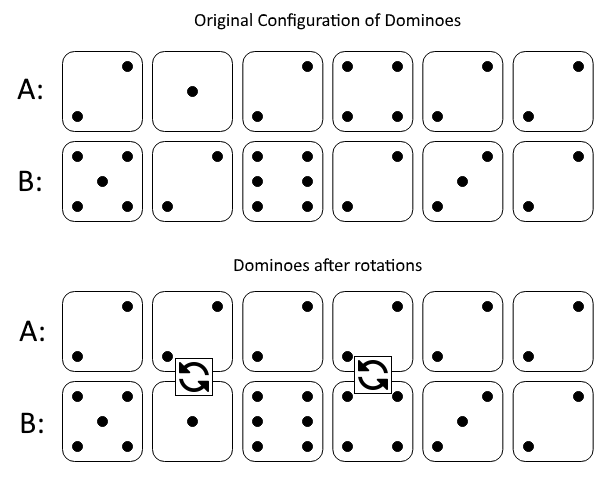
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
Explanation: 
The first figure represents the dominoes as given by A and B: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: A = [3,5,1,2,3], B = [3,6,3,3,4]
Output: -1
Explanation: 
In this case, it is not possible to rotate the dominoes to make one row of values equal.

 

Note:

1. 1 <= A[i], B[i] <= 6
2. 2 <= A.length == B.length <= 20000

A:

核心是先检查是否某个数字出现了n 次。  没有，则返回-1.

能，则检查每个target 数字，被A或者B所flip的个数

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

class Solution { public: int minDominoRotations(vector<int>& A, vector<int>& B) { int n = A.size(); if(n<=1) return 0; unordered_map<int,int> M; for(int i = 0;i<n;i++){ M[A[i]] ++; if(B[i] != A[i]){ M[B[i]]++; } } vector<int> V; for(int i =1;i<=6;i++){ if(M[i]==n){ V.push_back(i); } } if(V.size()==0) return -1; int res = n; for(auto k : V){ res = min(res, flip(A,k)); res = min(res, flip(B,k)); } return res; } private: int flip(vector<int> arr, int target){ int res =0; for(auto v : arr){ if(v!= target){ res++; } } return res; } };

其实。我们不需要map 的。 上面，我们用了map ,是因为我们觉得不知道是哪个target.

然而，其实只要看了第一个Domino, 我们就知道了。 就限定最多2个数字。

代码如下

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

class Solution { public: int minDominoRotations(vector<int>& A, vector<int>& B) { int n = A.size(); if(n<=1) return 0; int res =n; // check if match int canFind1 = true; for(int i =0;i<n;i++){ if(A[i]!= A[0] && B[i] != A[0]){ canFind1 = false; break; } } int canFind2 = true; for(int i =0;i<n;i++){ if(A[i]!= B[0] && B[i] != B[0]){ canFind2 = false; break; } } if( not canFind1 && not canFind2) return -1; if(canFind1){ res = min(res, flip(A,A[0])); res = min(res, flip(B,A[0])); } if(canFind2){ if(B[0] != A[0]){ res = min(res, flip(A,B[0])); res = min(res, flip(B,B[0])); } } return res; } private: int flip(vector<int> & A, int target){ int res = 0; for(auto v : A){ if(v!= target) res++; } return res; } };