You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.
If node i has no left child then leftChild[i] will equal -1, similarly for the right child.
Note that the nodes have no values and that we only use the node numbers in this problem.
Example 1:
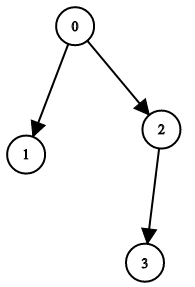
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1] Output: true
Example 2:
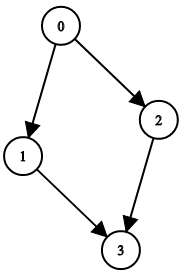
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1] Output: false
Example 3:
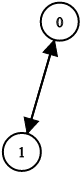
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1] Output: false
Example 4:
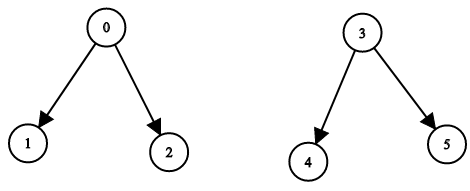
Input: n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1] Output: false
Constraints:
1 <= n <= 10^4leftChild.length == rightChild.length == n-1 <= leftChild[i], rightChild[i] <= n - 1
A:
思路是: 先看哪个node没有parent, 然后看从他开始,能否不重复地找到所有的Node.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | class Solution { public: bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) { // find the node without parent vector<bool> hasParent(n,false); for(int i =0;i<n;i++){ int ll = leftChild[i]; if(ll !=-1){ hasParent[ll] = true; } int rr = rightChild[i]; if(rr !=-1){ hasParent[rr] = true; } } int rootVal = -1; for(int i =0;i<n;i++){ if(not hasParent[i]){ rootVal = i; // there can exist more than one rootVal break; } } // now start from rootVal, all other node has parents. // dfs, make sure every node is visited only once vector<bool> visited(n,false); if(rootVal<0 || not dfs(leftChild, rightChild, visited, rootVal)){ return false; } // now check whether it have visited all nodes for(auto v:visited){ if(not v){ return false; } } return true; } private: bool dfs(vector<int>& leftChild, vector<int>& rightChild,vector<bool>& visited, int rootVal ){ if(rootVal <0) return true; if(visited[rootVal]) return false; visited[rootVal] = true; if(not dfs(leftChild, rightChild, visited, leftChild[rootVal])) return false; if(not dfs(leftChild, rightChild, visited, rightChild[rootVal])) return false; return true; } }; |
这个题做的比较糊涂。 哎, ~~~~~~~花了1个小时才做出来,悲伤~~~~
No comments:
Post a Comment