Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true
Example 2:
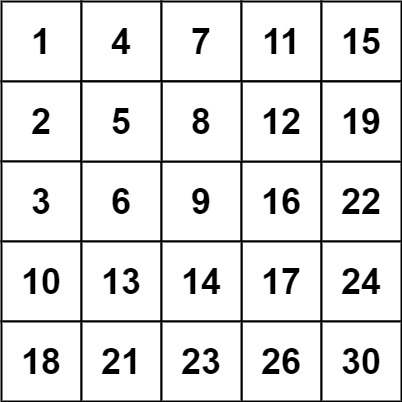
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-109 <= target <= 109
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 Output: true
Example 2:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-109 <= target <= 109
A:
思路是,对角线寻找。 复杂度 O(m+n)
如果从左上角开始,到一个点,如果A[i][i] > target了。 则不可能在右下角的区间。同样。也不能在左上角的区间。因此只可能在左下角和右上角的区间里
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
return helper(matrix,target, 0,0,m-1,n-1);
}
private:
bool helper(vector<vector<int>>& matrix, int target, int topX, int topY, int botX, int botY){ // bot -> bottom
if(topX > botX || topY > botY || matrix[topX][topY] > target){
return false;
}
// from [topX, topY] ,going diagnally ,to find a node that's bigger
int x = topX, y = topY;
while(x <= botX && y<= botY && matrix[x][y] <= target){
if(matrix[x][y] == target){
return true;
}
++x;
++y;
}
// now matrix[x][y] is bigger than target
return helper(matrix, target,topX, y, x-1, botY) || helper(matrix, target, x, topY,botX, y-1);
}
};
当然还有一种方法是逐行查找。 从右上角 开始 复杂度 O(m+n)
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
int i = 0,j=n-1;
while(i<m&& j>=0){
if(matrix[i][j] == target){
return true;
}else if(matrix[i][j] < target){
++i;
}else{
--j;
}
}
return false;
}
};
class Solution { public: bool searchMatrix(vector<vector<int>>& matrix, int target) { int m = matrix.size(), n = matrix[0].size(); return helper(matrix,target, 0,0,m-1,n-1); } private: bool helper(vector<vector<int>>& matrix, int target, int topX, int topY, int botX, int botY){ // bot -> bottom if(topX > botX || topY > botY || matrix[topX][topY] > target){ return false; } // from [topX, topY] ,going diagnally ,to find a node that's bigger int x = topX, y = topY; while(x <= botX && y<= botY && matrix[x][y] <= target){ if(matrix[x][y] == target){ return true; } ++x; ++y; } // now matrix[x][y] is bigger than target return helper(matrix, target,topX, y, x-1, botY) || helper(matrix, target, x, topY,botX, y-1); } };
class Solution { public: bool searchMatrix(vector<vector<int>>& matrix, int target) { int m = matrix.size(), n = matrix[0].size(); int i = 0,j=n-1; while(i<m&& j>=0){ if(matrix[i][j] == target){ return true; }else if(matrix[i][j] < target){ ++i; }else{ --j; } } return false; } };
No comments:
Post a Comment