1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance ---- M ~~~~~

There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.

Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.

Notice that the distance of a path connecting cities i and j is equal to the sum of the edges' weights along that path.

 

Example 1:

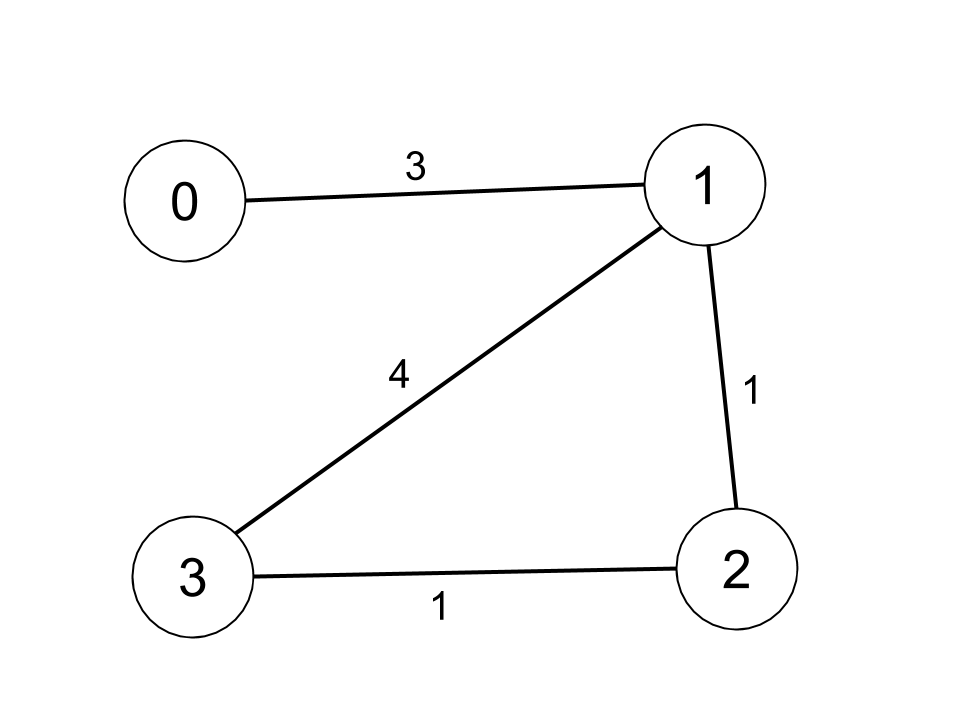
Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
Output: 3
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> [City 1, City 2] 
City 1 -> [City 0, City 2, City 3] 
City 2 -> [City 0, City 1, City 3] 
City 3 -> [City 1, City 2] 
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.

Example 2:

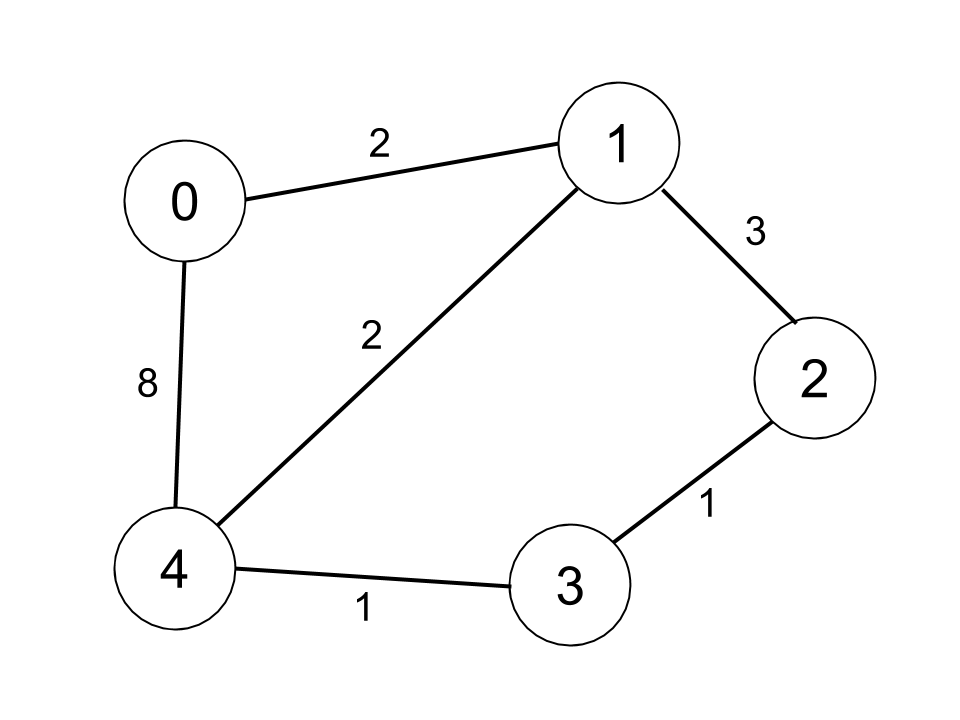
Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
Output: 0
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> [City 1] 
City 1 -> [City 0, City 4] 
City 2 -> [City 3, City 4] 
City 3 -> [City 2, City 4]
City 4 -> [City 1, City 2, City 3] 
The city 0 has 1 neighboring city at a distanceThreshold = 2.

 

Constraints:

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• All pairs (fromi, toi) are distinct.

A:

思想类似于 Floyd Warshall

我自己的思路是：

每次从vertex 开始做 BFS， 找到新的path cost更小的点，作为下一步的追踪可能。

class Solution {
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<vector<int>> V(n, vector<int>(n, INT_MAX));
        vector<vector<int>> M(n, vector<int>());  // M[i] = {neighbors}
        vector<int> NeighborCount(n,INT_MAX);
        for (auto edge : edges) {
            int a = edge[0], b = edge[1], w = edge[2];
            V[a][b] = w;
            V[b][a] = w;
            if (w <= distanceThreshold) {
                M[a].push_back(b);
                M[b].push_back(a);
            }
        }
        // mark every points as 0 to itself
        for (int i = 0; i < n; i++)
            V[i][i] = 0;

        for (int i = 0; i < n; i++) {
            //bfs
            auto curlayer = M[i];
            while (not curlayer.empty()) {
                vector<int> nextlayer;
                for (auto end : curlayer) {
                    if (V[i][end] <= distanceThreshold) {
                        for (auto newEnd : M[end]) {
                            int newDistance = V[i][end] + V[end][newEnd];
                            if (newDistance <= distanceThreshold && newDistance < V[i][newEnd]) {
                                V[i][newEnd] = newDistance;
                                nextlayer.push_back(newEnd);
                                M[i].push_back(newEnd);
                            }
                        }
                    }
                }
                curlayer = nextlayer;
            }
            unordered_set<int> tmp(M[i].begin(), M[i].end()); // remove duplicate
            NeighborCount[i] = tmp.size();
        }
        int minNeighborSize = *min_element(NeighborCount.begin(), NeighborCount.end());
        for (int i = n - 1; i >= 0; i--) {
            if (NeighborCount[i] == minNeighborSize)
                return i;
        }
        return -1;
    }
};

Errors：

1：  没有set  V[i][i] =0;  导致了多加了一些

2：  M[i] 一开始为了避免重复， 用了set, 然而iterator的时候很麻烦，我就改成了vector,可是后来忘记了去重。 

真正的Floy Warshal

class Solution {
public:
	int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
		vector<vector<int>> dp(n,vector<int>(n,INT_MAX/2));
		for(auto& x:edges){
			dp[x[0]][x[1]]=x[2];
			dp[x[1]][x[0]]=x[2];
		}
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				for(int k=0;k<n;k++){
					dp[j][k]=min(dp[j][k],dp[j][i]+dp[i][k]);
				}
			}
		}   
		int ans=-1;
		int cur=INT_MAX;
		for(int i=0;i<n;i++){
			int count=0;
			for(int j=0;j<n;j++){
				if(j!=i && dp[i][j]<=distanceThreshold){
					count++;
				}
			}
			if(count<=cur){
				cur=count;
				ans=i;
			}
		}
		return ans;
	}
};