587. Erect the Fence ------------ H ~!!!!! 三个解法

There are some trees, where each tree is represented by (x,y) coordinate in a two-dimensional garden. Your job is to fence the entire garden using the minimum length of rope as it is expensive. The garden is well fenced only if all the trees are enclosed. Your task is to help find the coordinates of trees which are exactly located on the fence perimeter.

 

Example 1:

Input: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output: [[1,1],[2,0],[4,2],[3,3],[2,4]]
Explanation: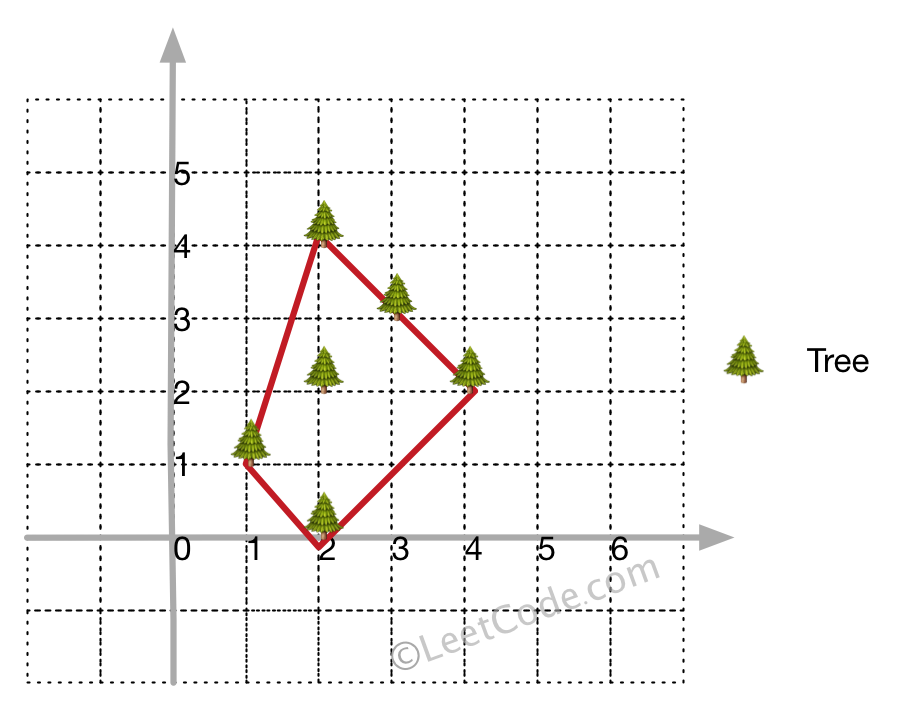

Example 2:

Input: [[1,2],[2,2],[4,2]]
Output: [[1,2],[2,2],[4,2]]
Explanation:

Even you only have trees in a line, you need to use rope to enclose them. 

 

Note:

1. All trees should be enclosed together. You cannot cut the rope to enclose trees that will separate them in more than one group.
2. All input integers will range from 0 to 100.
3. The garden has at least one tree.
4. All coordinates are distinct.
5. Input points have NO order. No order required for output.
6. input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.

A:

https://leetcode.com/problems/erect-the-fence/solution/

 Graham Scan

Algorithm

Graham Scan Algorithm is also a standard algorithm for finding the convex hull of a given set of points. Consider the animation below to follow along with the discussion.

The method works as follows. Firsly we select an initial point(

$bm$) to start the hull with. This point is chosen as the point with the lowest y-coordinate. In case of a tie, we need to choose the point with the lowest x-coordinate, from among all the given set of points. This point is indicated as point 0 in the animation. Then, we sort the given set of points based on their polar angles formed w.r.t. a vertical line drawn throught the intial point.

This sorting of the points gives us a rough idea of the way in which we should consider the points to be included in the hull while considering the boundary in counter-clockwise order. In order to sort the points, we make use of orientation function which is the same as discussed in the last approach. The points with a lower polar angle relative to the vertical line come first in the sorted array. In case, if the orientation of two points happens to be the same, the points are sorted based on their distance from the beginning point($bm$). Later on we'll be considering the points in the sorted array in the same order. Because of this, we need to do the sorting based on distance for points collinear relative to $bm$, so that all the collinear points lying on the hull are included in the boundary.

But, we need to consider another important case. In case, the collinear points lie on the closing(last) edge of the hull, we need to consider the points such that the points which lie farther from the initial point $bm$ are considered first. Thus, after sorting the array, we traverse the sorted array from the end and reverse the order of the points which are collinear and lie towards the end of the sorted array, since these will be the points which will be considered at the end while forming the hull and thus, will be considered at the end. Thus, after these preprocessing steps, we've got the points correctly arranged in the way that they need to be considered while forming the hull.

Now, as per the algorithm, we start off by considering the line formed by the first two points(0 and 1 in the animation) in the sorted array. We push the points on this line onto a $stack$. After this, we start traversing over the sorted $points$ array from the third point onwards. If the current point being considered appears after taking a left turn(or straight path) relative to the previous line(line's direction), we push the point onto the stack, indicating that the point has been temporarily added to the hull boundary.

This checking of left or right turn is done by making use of orientation again. An orientation greater than 0, considering the points on the line and the current point, indicates a counterclockwise direction or a right turn. A negative orientation indicates a left turn similarly.

If the current point happens to be occuring by taking a right turn from the previous line's direction, it means that the last point included in the hull was incorrect, since it needs to lie inside the boundary and not on the boundary(as is indicated by point 4 in the animation). Thus, we pop off the last point from the stack and consider the second last line's direction with the current point.

Thus, the same process continues, and the popping keeps on continuing till we reach a state where the current point can be included in the hull by taking a right turn. Thus, in this way, we ensure that the hull includes only the boundary points and not the points inside the boundary. After all the points have been traversed, the points lying in the stack constitute the boundary of the convex hull.