979. Distribute Coins in Binary Tree -------M

 Given the root of a binary tree with N nodes, each node in the tree has node.val coins, and there are N coins total.

In one move, we may choose two adjacent nodes and move one coin from one node to another.  (The move may be from parent to child, or from child to parent.)

Return the number of moves required to make every node have exactly one coin.

 

Example 1:

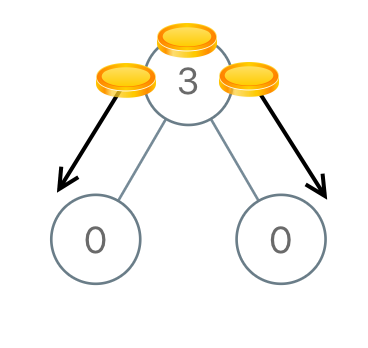
Input: [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

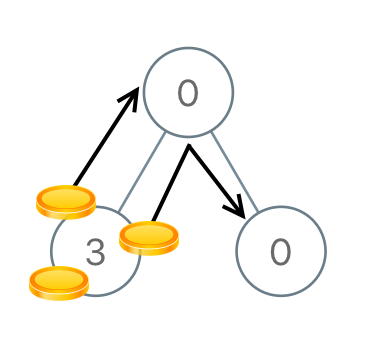
Input: [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves].  Then, we move one coin from the root of the tree to the right child.

Example 3:

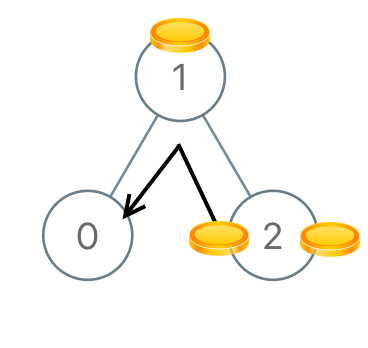
Input: [1,0,2]
Output: 2

Example 4:

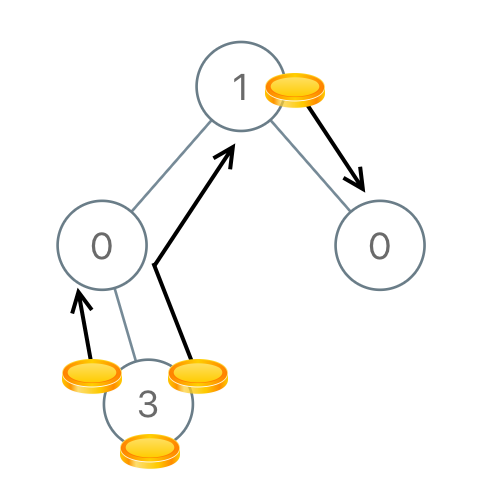
Input: [1,0,0,null,3]
Output: 4

 

Note:

1. 1<= N <= 100
2. 0 <= node.val <= N

A:

就是递归调用

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int distributeCoins(TreeNode* root) {
        int res = 0;
        helper(root, res);
        return res;
    }
private:
    int helper(TreeNode* root, int & res){// return number of coins it returned to parent of root
        if(not root)
            return 0;
        int ll = helper(root->left, res);
        int rr = helper(root->right, res);
        int cur = root->val + ll + rr -1;
        res += abs(ll) + abs(rr);
        return cur;
    }
};